[2023-동계모각코] 4회차 결과

- 강화학습 테트리스(tetr.io)에 적용해보기

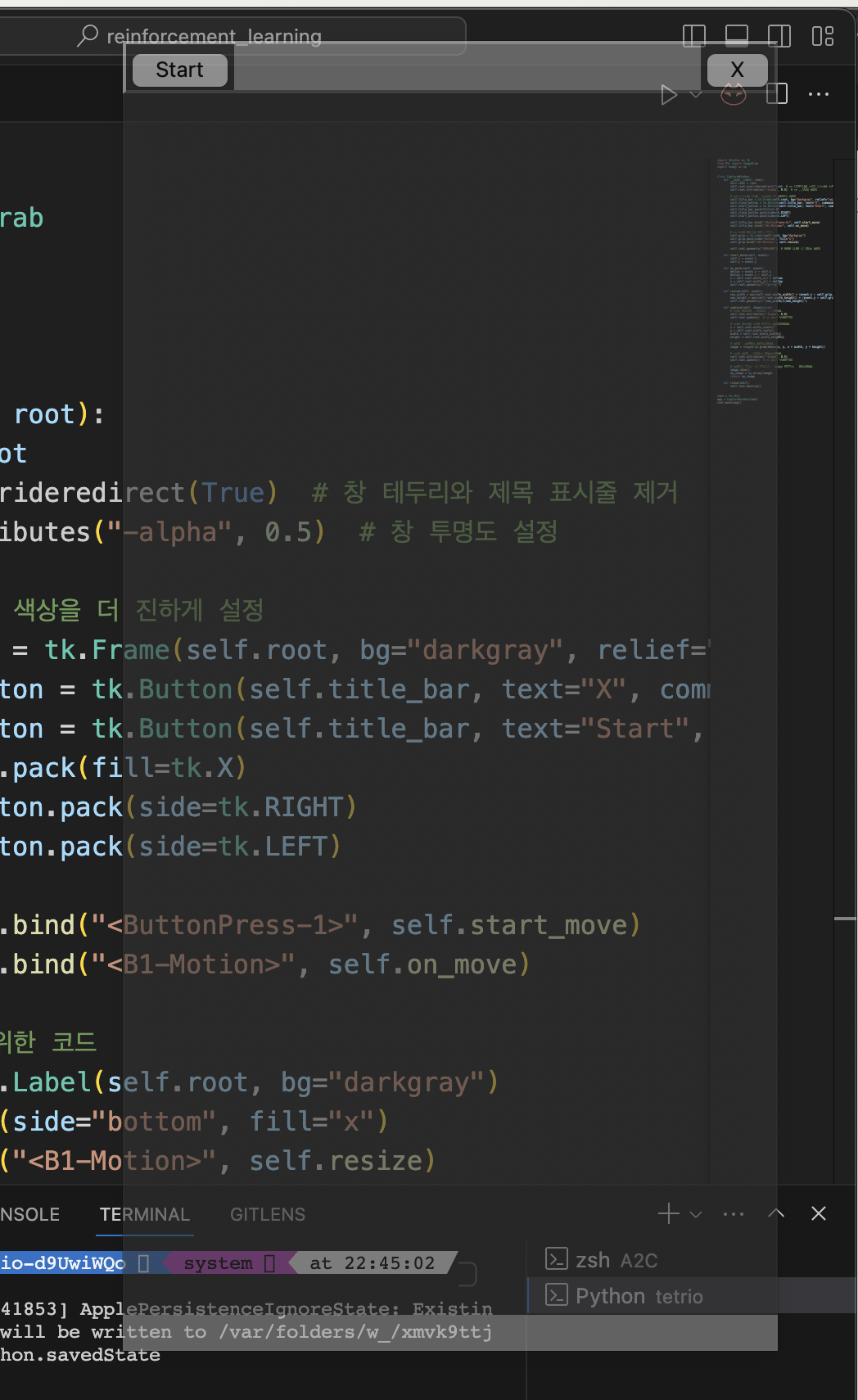
화면 캡처를 위한 토대를 구축하였다.

게임 화면 위치가 쉽게 변경될 수 있는 환경 특징 상, 유저가 쉽게 캡처 위치를 지정하도록 만들었다.

- 혁펜하임 강화학습 강의 정리하기

사용할 Bayesian Rule

$$
\begin{align}
p(x, y) = p(x | y)\ p(y) \
p(x, y | z) = p(x | y, z)\ p(y | z)
\end{align}
$$

상태 가치 함수 전개

$$
\begin{align}
V(s_t) &\ \dot= \int_{a_t: a_\infty} G_t\ p(a_t, s_{t+1}, a_{t+1}, \cdots |s_t) d_{a_t: a_\infty} \tag{1} \

& = \int_{a_t} \int_{s_{t+1}: a_\infty} G_t\ p(s_{t+1}, a_{t+1}, \cdots |s_t, a_t) d_{s_{t+1}: a_\infty}\ p(a_t | s_t) d_{a_t} \tag{2} \

& = \int_{a_t} Q(s_t, a_t)\ p(a_t | s_t) d_{a_t} \tag{3} \
\end{align}
$$

• 3번 수식의 의미
  • V는 Q를 상태 $s_t$에서의 모든 action에 대해 평균을 취하는 것이다.

$$
\begin{align}
V(s_t) &\ \dot= \int_{a_t: a_\infty} G_t\ p(a_t, s_{t+1}, a_{t+1}, \cdots |s_t) d_{a_t: a_\infty} \tag{1} \

&= \int_{a_t: a_\infty} (R_t + \gamma G_{t+1})\ p(a_t, s_{t+1}, a_{t+1}, \cdots |s_t) d_{a_t: a_\infty} \

&= \int_{a_t: a_\infty} (R_t + \gamma G_{t+1})\ p(s_{t+1}, a_{t+1}, s_{t+2}, \cdots | s_t, a_t)\ p(a_t|s_t) d_{a_t: a_\infty} \

&= \int_{a_t: a_\infty} (R_t + \gamma G_{t+1})\ p(a_{t+1}, s_{t+2}, \cdots | s_t, a_t, s_{t+1})\ p(a_t|s_t)\ p(s_{t+1} | s_t, a_t) d_{a_t: a_\infty} \

&= \int_{a_t: a_\infty} (R_t + \gamma G_{t+1})\ p(a_{t+1}, s_{t+2}, \cdots | s_{t+1})\ p(a_t|s_t)\ p(s_{t+1} | s_t, a_t) d_{a_t: a_\infty} \

&= \int_{a_t, s_{t+1}} \int_{a_{t+1}: a_\infty} (R_t + \gamma G_{t+1})\ p(a_{t+1}, s_{t+2}, \cdots | s_{t+1})d_{a_{t+1}: a_\infty} \ p(a_t|s_t)\ p(s_{t+1} | s_t, a_t) d_{a_t, s_{t+1}} \

&= \int_{a_t, s_{t+1}} \int_{a_{t+1}: a_\infty} R_t\ p(a_{t+1}, s_{t+2}, \cdots | s_{t+1}) + \gamma G_{t+1}\ p(a_{t+1}, s_{t+2}, \cdots | s_{t+1})\ d_{a_{t+1}: a_\infty} \&\qquad \qquad \qquad \qquad \ p(a_t|s_t)\ p(s_{t+1} | s_t, a_t) d_{a_t, s_{t+1}} \

&= \int_{a_t, s_{t+1}} \int_{a_{t+1}: a_\infty} R_t\ p(a_{t+1}, s_{t+2}, \cdots | s_{t+1})\ d_{a_{t+1}: a_\infty}\ p(a_t|s_t)\ p(s_{t+1}|s_t, a_t)\ d_{a_t, s_{t+1}} \
& \qquad + \int_{a_t, s_{t+1}} \int_{a_{t+1}: a_\infty} \gamma G_{t+1}\ p(a_{t+1}, s_{t+2}, \cdots | s_{t+1})\ d_{a_{t+1}: a_\infty}\ p(a_t|s_t)\ p(s_{t+1}|s_t, a_t)\ d_{{a_t}, s_{t+1}} \

&= \int_{a_t, s_{t+1}} \int_{a_{t+1}: a_\infty} R_t\ p(a_{t+1}, s_{t+2}, \cdots | s_{t+1})\ d_{a_{t+1}: a_\infty}\ p(a_t|s_t)\ p(s_{t+1}|s_t, a_t)\ d_{a_t, s_{t+1}} \
& \qquad + \int_{a_t, s_{t+1}} \gamma V(s_{t+1})\ p(a_t|s_t)\ p(s_{t+1}|s_t, a_t)\ d_{{a_t}, s_{t+1}} \

&= \int_{a_t, s_{t+1}} R_t\ p(a_t|s_t)\ p(s_{t+1}|s_t, a_t)\ d_{a_t, s_{t+1}} \
& \qquad + \int_{a_t, s_{t+1}} \gamma V(s_{t+1})\ p(a_t|s_t)\ p(s_{t+1}|s_t, a_t)\ d_{{a_t}, s_{t+1}} \

&= \int_{a_{t}, s_{t+1}} (R_t + \gamma V(s_{t+1}))\ p(a_t|s_t)\ p(s_{t+1}|s_t, a_t)\ d_{a_t, s_{t+1}} \tag2 \

&= \int_{a_t, s_{t+1}} (R_t + \gamma V(s_{t+1}))\ p(a_t, s_{t+1}|s_t)\ d_{a_t, s_{t+1}} \tag3

\end{align}
$$

• 3번 수식의 의미
  • $V(s_t)$는 $V(s_{t+1})$을 통해 구할 수 있다.
  • $s_t$에서 취할 수 있는 모든 $a_t$와, 그로부터 전이될 수 있는 $s_{t+1}$에서의 상태 가치 함수의 기댓값을 활용하여 현재 상태의 가치 함수를 계산할 수 있다.

행동 가치 함수 전개

$$
\begin{align}

Q(s_t, a_t) &\ \dot= \int_{s_{t+1}: a_\infty}G_t\ p(s_{t+1}, a_{t+1}, s_{t+2}, a_{t+2}, \cdots | s_t, a_t) d_{s_{t+1}: a_\infty} \tag{1} \

& = \int_{s_{t+1}} \int_{a_{t+1}: {a_\infty}}G_t\ p(a_{t+1}, s_{t+2}, a_{t+2}, \cdots | s_t, a_t, s_{t+1}) d_{a_{t+1}: a_\infty}\ p(s_{t+1} | s_t, a_t) d_{s_{t+1}} \tag{2} \

& = \int_{s_{t+1}} \int_{a_{t+1}: {a_\infty}}G_t\ p(a_{t+1}, s_{t+2}, a_{t+2}, \cdots | s_{t+1}) d_{a_{t+1}: a_\infty}\ p(s_{t+1} | s_t, a_t) d_{s_{t+1}} \tag3 \

& = \int_{s_{t+1}} \int_{a_{t+1}: {a_\infty}}G_t\ p(a_{t+1}, s_{t+2}, a_{t+2}, \cdots | s_{t+1}) d_{a_{t+1}: a_\infty}\ p(s_{t+1} | s_t, a_t) d_{s_{t+1}} \tag4 \

& = \int_{s_{t+1}} V(s_{t+1})\ p(s_{t+1} | s_t, a_t) d_{s_{t+1}} \tag5 \

\end{align}
$$

• 5번 수식의 의미
  • Q는 V를 상태 $s_t$에서 행동 $a_t$를 선택했을 때 전이될 수 있는 모든 다음 상태 $s_{t+1}$에 대해 평균을 취하는 것이다.
    $$
    \begin{align}
    Q(s_t, a_t) &\ \dot=\int_{s_{t+1}: a_\infty}G_t\ p(s_{t+1}, a_{t+1}, s_{t+2}, a_{t+2}, \cdots | s_t, a_t)\ d_{s_{t+1}: a_{\infty}} \tag1 \

&= \int_{s_{t+1}: a_{\infty}}G_t\ p(s_{t+2}, a_{t+2}, \cdots | s_{t+1}, a_{t+1})\ p(s_{t+1}|s_t, a_t)\ p(a_{t+1}|s_{t+1}) \ d_{s_{t+1}: a_{\infty}} \

&= \int_{s_{t+1}: a_{\infty}} (R_t + \gamma G_{t+1}) p(s_{t+2}, a_{t+2}, \cdots | s_{t+1}, a_{t+1})\ p(s_{t+1}|s_t, a_t)\ p(a_{t+1}|s_{t+1})\ d_{s_{t+1}: a_{\infty}} \

&= \int_{s_{t+1}, a_{t+1}} \int_{s_{t+2}: a_{\infty}} (R_t + \gamma G_{t+1}) p(s_{t+2}, a_{t+2}, \cdots | s_{t+1}, a_{t+1})\ p(s_{t+1}|s_t, a_t)\ \ & \qquad p(a_{t+1}|s_{t+1})\ d_{s_{t+2}: a_{\infty}} \ d_{s_{t+1}, a_{t+1}} \

&= \int_{s_{t+1}, a_{t+1}} (R_t + \gamma Q(s_{t+1}, a_{t+1}))\ p(s_{t+1}|s_t, a_t)\ p(a_{t+1}|s_{t+1})\ d_{s_{t+1}, a_{t+1}} \tag2 \

&= \int_{s_{t+1}, a_{t+1}} (R_t + \gamma Q(s_{t+1}, a_{t+1}))\ p(s_{t+1}, a_{t+1}|s_t, a_t)\ d_{s_{t+1}, a_{t+1}} \tag3 \
\end{align}
$$

• 3번 수식의 의미
  • $Q(s_t, a_t)$는 $Q(s_{t+1}, a_{t+1})$를 이용하여 구할 수 있다.
  • $s_t$에서 $a_t$를 선택했을 때, 전이될 수 있는 상태인 $s_{t+1}$과 그 상태에서 고를 수 있는 모든 $a_{t+1}$에서 행동 가치 함수의 기댓값을 활용하여 현재 행동의 가치 함수를 계산할 수 있다.